Source: web.mit.edu
When you’re declaring a bridge hand, it’s beneficial to know some simple odds about the chances for favorable suit breaks and finesses. This knowledge will help you estimate the potential number of tricks you can take in a specific suit combination.
Knowing the odds will also help you decide which overall line of play you should take to make your contract. For example, if you have to choose between playing for a 7-card side suit to break 3-3 or taking a successful finesse, you’ll know that the finesse is a better bet (50%) than the suit break (36%).
Odds of suit breaks: In general: An ODD number of missing cards will tend to break evenly — if you are missing 5 cards in a suit, they will divide 3-2 more often than 4-1.
An EVEN number of missing cards will tend to break UNevenly — if you are missing 6 cards in a suit, they will divide 4-2 more often than 3-3.
If you have a combined fit of 7 cards in a suit (your opponents have 6):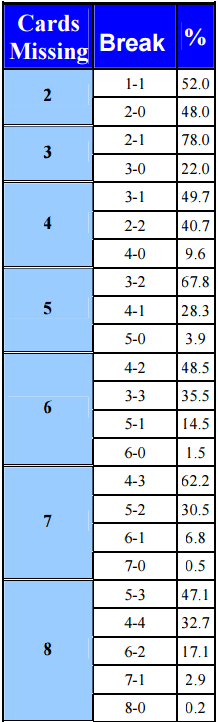
3-3 break = 36%
4-2 = 48%
5-1 = 15%
6-0 = 1%
You have 8, they have 5:
3-2 = 68%
4-1 = 28%
5-0 = 4%
You have 9, they have 4:
2-2 = 40%
3-1 = 50%
4-0 = 10%
You have 10, they have 3:
2-1 = 78%
3-0 = 22%
Finding honors:
Your expected percentage of success when you need:
One finesse = 50%
One of two finesses = 75%
Two of two finesses = 25%
At least two of three finesses = 50%
The presence of spot cards (10’s and 9’s) will often increase your odds of finding or dropping honors:
AKQ10 opposite xxx = 61% chance of 3 tricks (because when the suit breaks 4-2 or 5-1, the jack may drop singleton or doubleton).
AJ98 opposite xxx = 38% chance of 3 tricks (finesse the 9 first, which wins when K10, Q10 or KQ10 are onside).
Esta entrada también está disponible en: Spanish

